Coefficient of performance

Figure 1. The heating coefficient of performance of a system (heat pump) is the ratio of heat delivered to the hot reservoir to the work put into the system.

Figure 2. The cooling coefficient of performance of a system (refrigerator, air conditioning) is the ratio of heat out of the cold reservoir to the work put into the system.

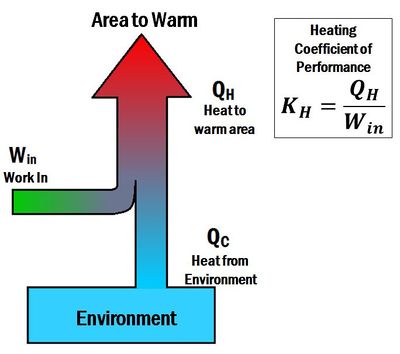
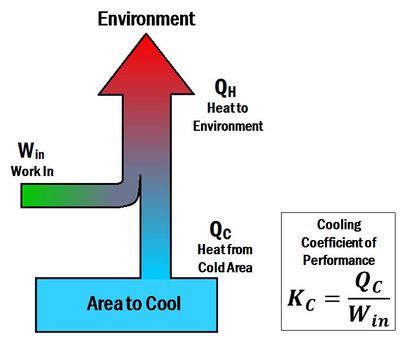
The Coefficient of performance (K or COP) is a number that describes the effectiveness of heat pumps, refrigerators or air conditioners. The coefficient of performance is different for heating and cooling systems. For a heat pump (a heating system), the coefficient of performance is the ratio of energy delivered to the hot reservoir to the work input. Thus, it is called a heating coefficient of performance ([math]K_{heating}[/math]). In contrast, for a refrigerator or an air conditioner (cooling systems), the coefficient of performance is a ratio of energy taken away from the cold reservoir to the work input. Thus, it is called a cooling coefficient of performance ([math]K_{cooling}[/math]). When a heat pump is operated in reverse, it acts like a refrigerator. The term energy efficiency ratio (EER) can be used to describe the cooling coefficient of performance of a heat pump operating in reverse.

The coefficient of performance for both heating and cooling is similar to the thermal efficiency of heat engines. This is because they relate what benefits you are getting out of the system (i.e. work, heating or cooling) to what you had to pay.

The coefficient of performance for heating is given by the equation:

[math]K_{heating}=\frac{Q_H}{W_{in}}[/math]

where:

• [math]Q_H[/math] is the heat delivered by the heat pump
• [math]W_{in}[/math] is the work input to the system
• [math]K_{heating}[/math] is the heating coefficient of performance

The coefficient of performance for cooling is given by the equation:

[math]K_{cooling}=\frac{Q_C}{W_{in}}[/math]

where:

• [math]Q_C[/math] is the heat dispelled from the refrigerator
• [math]W_{in}[/math] is the work input to the system
• [math]K_{cooling}[/math] is the cooling coefficient of performance

A better heat pump will require require less work to deliver a given amount of heat. Similarly, a better refrigerator will require require less work to remove a given amount of heat. Thus, better heat pumps and refrigerators will have larger coefficients of performance. From the equation, it is clear that if no work was put into the system ([math]W_{in}=0[/math]) the coefficient would equal infinity. This would constitute a perfect heat pump or refrigerator, which is forbidden by the Second law of thermodynamics. Hence, [math]K\lt \infty[/math].

Maximum Coefficient of Performance

Just like there is a thermal Carnot efficiency, there is also a Carnot coefficient of performance. This maximum coefficient of performance depends on the temperatures of the hot and cold reservoirs of the system. The equation for the Carnot coefficient of performance is different for a heating system (like a heat pump) versus a cooling system (like a refrigerator).

The Carnot coefficient of performance for heating is given by the equation:

[math]K_{H_{Carnot}}=\frac{T_H}{T_H-T_C}[/math]

where:

• [math]T_H[/math] is the temperature of the space to which the heat is delivered
• [math]T_C[/math] is the temperature of the environment that heat is taken from
• [math]K_{H_{Carnot}}[/math] is the maximum coefficient of performance for a heat pump

The Carnot coefficient of performance for cooling is given by the equation:

[math]K_{C_{Carnot}}=\frac{T_C}{T_H-T_C}[/math]

where:

• [math]T_H[/math] is the temperature of the environment to which the heat is dispelled to
• [math]T_C[/math] is the temperature of the space to cool off
• [math]K_{C_{Carnot}}[/math] is the maximum coefficient of performance for a refrigerator or an air conditioner

Coefficient of Performance Video

This video explains the difference between the heating coefficient of performance and the cooling coefficient of performance with an example calculation of each.

For Further Reading

• Heat pump
• Refrigerator
• Heat engine
• Efficiency
• Carnot efficiency
• Or explore a random page