Rendement de Carnot
Le rendement de Carnot décrit le rendement thermique maximal qu'un machine thermique peut atteindre, selon la Deuxième loi de la thermodynamique. Cette loi a été dérivée par Sadi Carnot en 1824.Carnot a étudié l'idée du rendement maximal d'un machine thermique, demandant si le rendement d'une machine thermique peut approcher 100 %, ou s'il existe une limite à ne pas dépasser. [2] La réponse s'est avérée être qu'il existe une valeur maximale, et Carnot a développé un moteur idéal qui donnerait théoriquement ce rendement, connu sous le nom de moteur de Carnot. Le rendement maximal, connu sous le nom de rendement de Carnot [math]\displaystyle{ \eta_{max} }[/math], ne dépend que des températures de la source chaude et du puits froid [math]\displaystyle{ T_H }[/math] et [math]\displaystyle{ T_L }[/math], comme le montre la figure 1, et est donné par l'équation ci-dessous.[3]
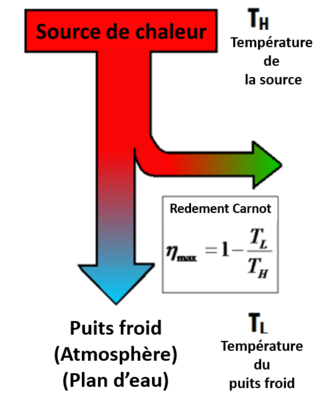
(1)
La deuxième loi exige que la chaleur résiduelle soit produite dans un processus thermodynamique où le travail est effectué par une source de chaleur. Un tel processus est donné par l'équation
(2)
Avec un rendement thermique de
(3)
Où :
- [math]\displaystyle{ Q_H }[/math] est la chaleur fournie au système par un combustible
- [math]\displaystyle{ Q_L }[/math] est la chaleur dégagée par le système vers le puits froid, appelée chaleur résiduelle
- [math]\displaystyle{ W }[/math] est le travail utile effectué par le système
Par conséquent, le rendement de Carnot donne une quantité maximale de travail atteignable pour tout machine thermique. L'équation 1 montre qu'en augmentant [math]\displaystyle{ T_H }[/math] ou en diminuant [math]\displaystyle{ T_L }[/math], le rendement peut être augmenté. L'idéal serait donc de rendre la température du puits froid égale au zéro absolu, mais on sait que c'est un exploit impossible. En réalité, le puits froid est l'environnement de la Terre. Cela signifie que le puits froid est à une température d'environ 310 Kelvin, et que les sources chaudes que nous pouvons obtenir dans les moteurs thermiques à partir de la combustion de carburants brûlent à une température d'environ 650 Kelvin. Ces températures donnent une valeur de rendement de Carnot de [math]\displaystyle{ \eta_{max}=0,52 }[/math].[4]
Moteur de Carnot
Un moteur de Carnot est un moteur idéalisé, utilisant des processus dont les interactions mécaniques et thermiques sont réversibles. Cela signifie que le moteur peut effectuer ses mouvements et revenir à son état initial sans augmentation de l'entropie (sans perte d'énergie). Pour que le moteur puisse revenir à son état initial sans augmenter l'entropie, le moteur doit être en équilibre thermique tout au long de son cycle. Les conditions pour qu'un tel moteur existe sont :[2]
- Interactions mécaniques :aucune énergie n'est perdue sous forme de friction, il n'y a donc aucun transfert de chaleur au cours de ces processus mécaniques ([math]\displaystyle{ Q=0 }[/math]), ce que l'on appelle un processus adiabatique.
- Interactions thermiques : le transfert de chaleur est infiniment lent (connu sous le nom de quasi-statique). Cela signifie que la différence de température entre le système et la chaleur d'entrée/sortie est presque la même, ce qui fait que le transfert de chaleur s'effectue sur un temps infini. Ces échanges doivent se faire en maintenant la température interne du système constante, ce que l'on appelle un processus isotherme.
Un moteur qui ne possède que ces propriétés est connu sous le nom de moteur de Carnot, qui est un moteur parfaitement réversible, et qui présente l'efficacité thermique maximale ([math]\displaystyle{ \eta_{max} }[/math]) et, s'il fonctionne comme un réfrigérateur, le coefficient de performance ([math]\displaystyle{ K_{max} }[/math]). Bien qu'un tel moteur maximiserait le rendement, en termes de résultats, il est terriblement inutile puisque ses processus idéalisés prennent tellement de temps pour produire une quantité significative de travail. Comme le dit Schroeder, ne vous donnez pas la peine d'installer un moteur de Carnot dans votre voiture ; cela améliorerait votre consommation d'essence, mais vous vous feriez doubler par des piétons.[5]
Pour en savoir plus sur le moteur de Carnot, visitez le site NASA ou hyperphysics.
Références
- ↑ Wikimedia Commons [Online], Available: http://upload.wikimedia.org/wikipedia/en/a/a2/Heat_engine.png
- ↑ 2,0 et 2,1 R. D. Knight, "The Limits of Efficiency" in Physics for Scientists and Engineers: A Strategic Approach, 3nd ed. San Francisco, U.S.A.: Pearson Addison-Wesley, 2008, ch.19, sec.5, pp. 540-542
- ↑ Hyperphysics, Carnot Cycle [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/carnot.html
- ↑ R. Wolfson, "Entropy, Heat Engines, and the Second Law of Thermodynamics" in Energy, Environment, and Climate, 2nd ed., New York, NY: W.W. Norton & Company, 2012, ch. 4, sec. 7, pp. 81-84
- ↑ McMaster Physics and Astronomy, Carnot Cycle [Online], Available: http://www.physics.mcmaster.ca/~morozov/3K03/Lecture9.pdf

