Work-energy theorem

The work-energy theorem explains the idea that the net work - the total work done by all the forces combined - done on an object is equal to the change in the kinetic energy of the object. After the net force is removed (no more work is being done) the object's total energy is altered as a result of the work that was done.

This idea is expressed in the following equation:

[math]W_{net} = \Delta K = K_{f} - K_{i}[/math]

• [math]W[/math] is the total work done
• [math]\Delta K[/math] is the change in kinetic energy
• [math]K_{f}[/math] is the final kinetic energy
• [math]K_{i}[/math] is the initial kinetic energy

For more information on this and other concepts related to work and energy, see Hyperphysics.

Figure 1. In the top image, positive work is done as a force is applied in the direction of movement, resulting in an increase in velocity and kinetic energy. In the bottom image, negative work is done as a force is applied against the direction of movement, resulting in a decrease in velocity and kinetic energy.

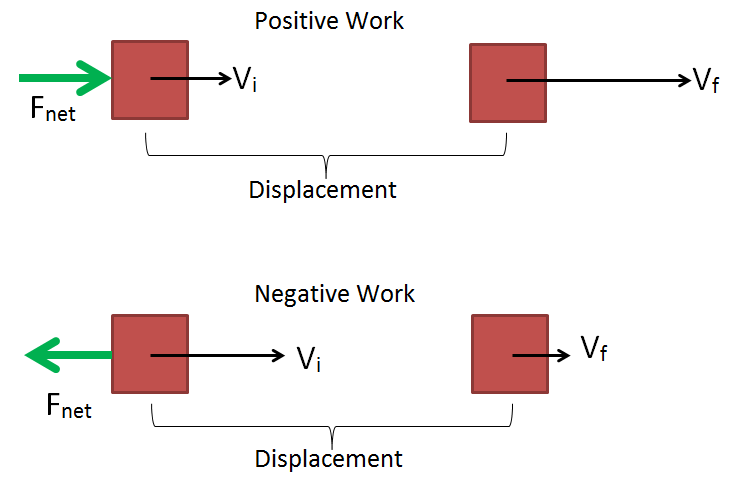
Example

To further understand the work-energy theorem, it can help to look at an example. Imagine a skier moving at a constant velocity on a flat, frictionless surface. If someone comes up behind him and pushes them for a distance - essentially doing work on the skier - then they will speed up as a result of their kinetic energy increasing. This type of working is known as positive work since the force was applied in the motion of the skier. If however the person pushed opposite to the skiers motion, the skier would slow down as a result of their kinetic energy decreasing. This type of work is known as negative work. The visual above shows an example of such a situation, just with the skier replaced by a block.

Since in reality there are no frictionless surfaces, the friction force opposing the skiers motion would have to be accounted for and this is why the equation contains the term W_net, as it is a sum of all the forces acting over a distance.