Logarithmic scale
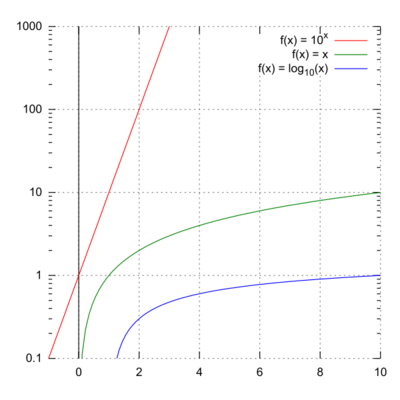
A logarithmic scale is a nonlinear scale often used when analyzing a large range of quantities. Instead of increasing in equal increments, each interval is increased by a factor of the base of the logarithm. Typically, a base ten and base e scale are used.
A basic equation for a base ten logarithmic plot is
which can be rearranged to
What this means is that for every one value of y, the value of x will increase by a factor of ten, and vice versa. Using a logarithmic scale can be useful when creating graphs to compress the scale and make the data easier to comprehend. When plotted on a semi-log plot, seen in Figure 1, the exponential 10x function appears linear, when it would normally diverge quickly on a linear graph.
This is useful for many applications, some of which will be seen below.
Examples
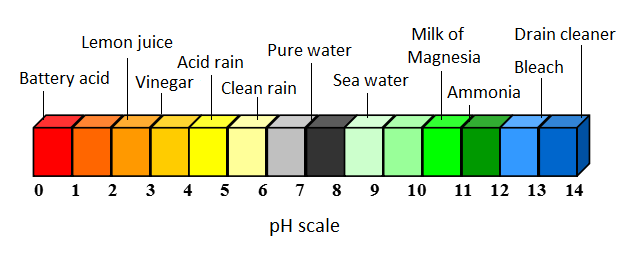
- The pH scale - A commonly used logarithmic scale is the pH scale, used when analyzing acids and bases. What the pH scale is doing is measuring the concentration of hydrogen ions (H+) in a substance, and is given by the equation
- By this, for every one decrease (due to the negative sign) in the pH, the acidity increases by a factor of ten (A pH of 3 is 10 times more acidic than a pH of 4, and is 100 times more acidic than a pH of 5).
- Sound - The way sound is picked up by one's ears is of logarithmic nature. The decibel (dB) system of sound intensity is a measure of how loud a sound is to one's ears. It is represented by the equation
- where is the threshold of hearing and is the intensity of the sound.[3] A conversation is roughly 1 million times more intense than the threshold value. The corresponding decibel value is then
- Now, if two people are talking at once, that only raises the dB to 63 dB. So a doubling of sound intensity just leads to +3dB. The threshold of pain is about 120 dB and that causes hearing loss.
- The Richter Scale - Earthquakes are measured on the Richter Scale, which is a base 10 logarithmic scale. This scale measures the magnitude of an earthquake, which is the amount of energy released by it. For every single increase on this scale, the magnitude is increased by a factor of 10.[4] Visit HowStuffWorks to learn more.
References
- ↑ Wikimedia Commons [Online], Available: https://upload.wikimedia.org/wikipedia/commons/4/46/LogLinScale.svg
- ↑ Created internally by a member of the Energy Education team: Adapted from Energy: Its use and the Environment.
- ↑ Hyperphysics. (August 25, 2015). Decibels [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/sound/db.html
- ↑ Harris, Tom, and Patrick J. Kiger. (August 24, 2015). "How Earthquakes Work". HowStuffWorks.com [Online], Available: http://science.howstuffworks.com/nature/natural-disasters/earthquake.htm

