The pH scale
The term pH is an abbreviation for power of Hydrogen, which is a measure of how acidic or basic a chemical solution is. Most solutions are either acidic or basic (also called "alkaline") - a substance that is neither acidic nor a basic is "neutral".[2]
Acids and bases are very important chemically, and are found almost everywhere. One example in the context of energy is acid rain, which is formed when water interacts with various pollutants in the atmosphere. Pollutants dissolved in the rain water cause it to be acidic, which can cause damage to the environment and man-made structures. Read more about acid rain here.
The pH scale
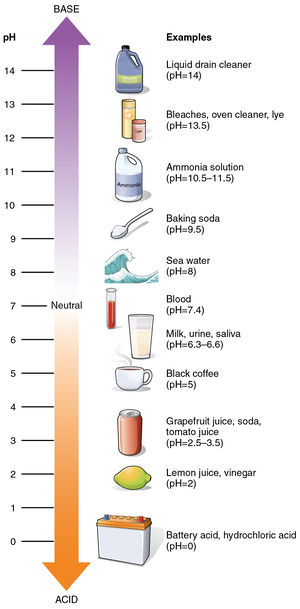
A pH value is used to describe a water-based solution. In general, a small pH value describes a solution that is acidic, and a larger pH value describing solutions that are less acidic (more basic). The pH scale is centered on 7 - meaning that a solution with a pH of 7 is perfectly neutral (neither acidic nor basic). Some examples of common substances and their place on the pH scale is shown in Figure 1.
The pH value of a solution directly measures the concentration of hydrogen ions (H+) in the solution. Acids have a large H+ concentration, which translates to a small pH value. Bases have very little H+. Basic solutions have large pH values - greater than pH 7.
While pH values have been measured as low as -3.6[3] and as high as 17.6 [4], most solutions encountered in nature range between pH 0 to pH 14.
pH is a logarithmic scale. This means that for each one-digit change in pH, the acidity (H+ concentration) changes by 10 times. For example, a solution with a pH of 4 has 10 times more H+ than a solution with a pH of 5. A solution of pH 3 will have 100 times more H+ (it is 100 times more acidic) than a solution of pH 5.
Hydroxide and Hydrogen Ions
Since pH is measured in water-based solutions, there is always a balance between H+ (hydrogen ions) and OH– (hydroxide ions). This is because water can break down into these two ions:
At room temperature, the balance between the H+ and OH– concentrations in water are related by this expression ([H+] means "concentration of H+"):
This equation shows that the more hydrogen ions a solution has, the fewer hydroxide ions it must have. So: an acidic solution that has a large amount of H+ will have very little OH–. And a basic solution that has very little H+ will have more OH–. A solution that is exactly neutral will have the same amount of H+ and OH–.
Calculating pH
To calculate pH, you should know the concentration of hydrogen ions (H+) in your solution. From there, the pH can be found by:
Since this is a logarithmic calculation, in order to change the pH by one unit (say, from 2 to 3), the concentration of H+ must be changed by 10 times (say, from 0.01 mol/L to 0.001 mol/L).
Discover More
The PhET simulation below was graciously provided by the University of Colorado. This simulation can help explore how pH changes as liquids mix.
For Further Reading
- Acid
- Base
- Chemical
- Water
- Acid rain
- Water cycle
- Or explore a random page
To explore pH further please see the Chemistry LibreTexts page.
References
- ↑ Wikimedia Commons [Online], Available: https://upload.wikimedia.org/wikipedia/commons/2/23/216_pH_Scale-01.jpg
- ↑ US EPA. (July 8, 2015). What is pH? [Online], Available: http://www.epa.gov/acidrain/measure/ph.html
- ↑ Nordstrom and Alpers, Negative pH, efflorescent mineralogy, and consequences for environmental restoration at the Iron Mountain Superfund site, California Proc Natl Acad Sci U S A, vol. 96, no. 7, pp 3455-3462, 1999 [Online], Available: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC34288/
- ↑ Licht, "pH Measurement in Concentrated Alkaline Solutions" Anal. Chem., vol. 57, pp. 514-519, 1985 [Online], Available, http://pubs.acs.org.ezproxy.lib.ucalgary.ca/doi/pdf/10.1021/ac50001a045

