Nonlinearity
Nonlinearity is a property that is used to describe a relationship that is not linear - essentially it is a term used to describe a relationship that cannot be plotted as a straight line on a graph, but rather has a curved or angular shape. The term however usually implies that the relationship will yield surprising results. More specifically non-linearity is a type of relationship that cannot be explained as a simple linear combination or sum of its variable inputs, instead it has some other relationship that could be logarithmic or based on a power relationship.[2] Nonlinearity in a relationship is the opposite of linearity.
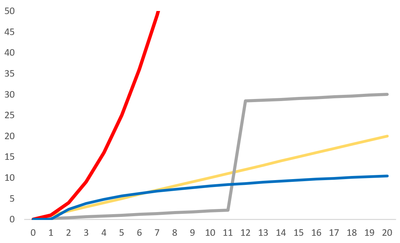
One of the biggest concerns about climate change is that some responses to increased greenhouse gases will be linear for a while, but will then have a sudden jump. These sudden jumps are often irreversible. This kind of relationship is shown with the grey line in Figure 1. Other relationships shown here are power relationships - shown in red - which is more than linear, as well as logarithmic in blue. This relationship shows a potential situation wherein more greenhouse gases being added to the atmosphere has comparatively less impact than a strictly linear relationship.
Importance
Nonlinearity can sometimes be an issue when cause and effect relationships are investigated as they cannot be predicted and modelled as easily as linear relationships. Instead, nonlinear cause-effect relationships require complex modeling and predictions to be able to explain some events.[3] Many nonlinear relationships are monotonic, meaning they always increase or decrease. These monotonic increases or decreases may be smooth or abrupt, again contributing to the difficulty in modelling nonlinear relationships.
Types
Some simple examples of nonlinear relationships are logarithmic relationships (), exponential relationships (), and power relationships (). Often times it is useful to generalize nonlinear relationships to a power law relationship, wherein every time you double one quantity you increase the other quantity by some number that is not two, but is always the same number.[3]
References
- ↑ Wikimedia Commons. (November 15, 2015). Resistor VI Graph [Online]. Available: https://upload.wikimedia.org/wikipedia/commons/2/20/Resistor_v-i_graph_(nonlinear).svg
- ↑ Oxford English Dictionary, online: http://www.oed.com/view/Entry/127994?redirectedFrom=nonlinear#eid Accessed October 17th, 2017.
- ↑ 3.0 3.1 New England Complex Systems Institute. (November 15, 2015). Concepts: Linear and Nonlinear

