Cross-sectional area
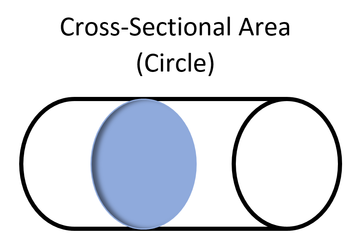
The cross-sectional area is the area of a two-dimensional shape that is obtained when a three-dimensional object - such as a cylinder - is sliced perpendicular to some specified axis at a point.[2]
For example, the cross-section of a cylinder - when sliced parallel to its base - is a circle. Thus, the cross-sectional area of this slice is the area of a circle with the radius equal to the radius of the provided cylinder.
Uses
The cross-sectional area of some shape is important in many different applications. The cross-section of a series of pipes carrying water helps to determine the speed and pressure with which the water flows through the pipe, especially if there is some change in the cross-sectional area of the pipe at some point. Using Bernoulli's equation, changes in the cross-sectional area of a pipe can be used to determine how other variables such as water pressure and speed must change to accommodate for this pipe change. As a result of this, cross-sectional area of pipes must be taken into account when building hydroelectric dams - particularly the penstocks - for hydroelectric power generation.
Additionally, the cross-sectional area is important when looking at nuclear reactions. The cross-section of some nucleus is used to define the effective size of a nucleus, and thus this value can be used to express the probability of some nuclear reaction taking place.[3] As well, the neutron cross section is particularly important as it expresses how likely a reaction between a neutron and a target nucleus is, the basis for nuclear fission.
For Further Reading
- Nuclear fission
- Tidal stream generator
- Wind power
- Bernoulli's equation
- Betz limit
- Or explore a random page
References
- ↑ Created internally by a member of the Energy Education team.
- ↑ Math Captain. (January 9, 2016). Cross Section [Online]. Available: http://www.mathcaptain.com/geometry/cross-section.html
- ↑ HyperPhysics. (January 9, 2016). Nuclear Reactions [Online]. Available: http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/nucrea.html

