Elastic potential energy
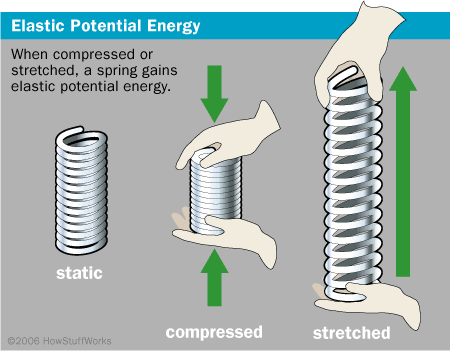
Elastic potential energy is the potential energy stored by the deformation of an elastic material, such as a spring seen in Figure 1.[2]
Background
The ability to transfer energy to this form depends on a material's elasticity. The energy stored in a spring depends on the:
- Distance the spring is deformed (stretched or compressed.)
- Spring constant. This constant is the amount of force required to stretch or compress a spring by one meter.[3]
Elastic potential energy is given by the equation:[3]
where
• : elastic potential energy (Joules, J)
• : spring constant (Newtons per meter, N/m)
• : distance from original (equilibrium) position (meters, m)
The elastic properties of a spring depend on both the shape and the material of the spring. Therefore, the spring constant is different for every object.
Application
Because a spring can remain in a compressed or stretched state for extended periods without dissipating energy, elastic potential energy is fundamental to many mechanical devices,[3] such as shock absorbers in cars.
This potential can also be utilized in control or mechanical systems to reduce the impact of disturbance, such as in motor vehicles. In vehicles, shock absorbers aim to reduce the impact on passengers by absorbing forces caused by driving on bumpy roads. Another use of elastic potential energy in vehicles is in regenerative braking systems, where stored energy is used to give the vehicle a small power boost.
Elastic vs. plastic deformation
Elastic deformation is a type of deformation that occurs when the energy used to change the shape of an object is equally output when pressures and forces are released. For example, when you pull a spring, the spring will return to its original shape when released (energy input equals energy output.) This is what allows objects to have elastic potential energy.
Plastic deformation is the type of deformation that occurs when the energy used to deform an object is not equal to energy output. The object does not return to its original shape. For example, when two cars collide, much of their kinetic energy is transferred into new forms and is used to permanently change the shape of the cars.[4]
Plasticity means that when something is stretched, it stays stretched. When an object stays stretched (or bent), that process is called plastic deformation. When the material goes back to its original form, elastic deformation has occurred.[5]
All springs have some degree of plastic deformation. Some energy is always transferred to new forms, such as thermal energy. Plastic deformation causes the atoms in the spring to speed up, raising the temperature of the material (similar to, but different from friction.) This is why the hoods of cars are quite hot after a car accident. Elastic potential energy does not transfer into new forms, so it does not increase the temperature.
Phet Simulation
The University of Colorado has graciously allowed us to use the following Phet simulation. Explore this simulation to see how gravitational potential energy, elastic potential energy, and kinetic energy are related in elastic systems.
For Further Reading
For further information please see the related pages below:
- Elasticity vs plasticity
- Mechanical energy
- Kinetic energy
- Potential energy
- Force
- Or explore a random page
- One can also visit hyperphysics.
References
- ↑ Wilson, Tracy. (2014, Aug. 14). How Crossbows Work [Online]. Available: http://science.howstuffworks.com/crossbow2.htm
- ↑ Landau, L.D. and Lifshitz, E. M., Theory of Elasticity, 3rd ed. Oxford, England: Butterworth Heinemann, 1986, Ch. 2.
- ↑ 3.0 3.1 3.2 R. D. Knight, "Springs," in Physics for Scientists and Engineers: A Strategic Approach, 2nd ed. San Francisco: Pearson Addison-Wesley, 2008, pp. 281-284.
- ↑ R. D. Knight, "Inelastic collisions," in Physics for Scientists and Engineers: A Strategic Approach, 2nd ed. San Francisco: Pearson Addison-Wesley, 2008, pp. 284-287.
- ↑ Hawkes et al, "Deformation and Elasticity," in Physics for Scientists and Engineers 1st ed. Toronto: Cengage, 2014, pp. 265-268.

