Venturi effect
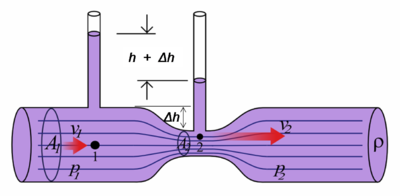
The Venturi effect describes how the velocity of a fluid increases as the cross section of the container it flows in decreases (like when flowing through a funnel). The energy in this increased speed comes by reducing the static pressure of the fluid. In the case of tidal stream generators, a duct or shroud (otherwise known as a diffuser) can be used to increase the amount of power available. As seen in Figure 2, a funnel shape is built around or near the turbine that causes the flow rate of the water to increase. These tubes speed up the water flow, which makes for a greater power output than a similar sized turbine without a shroud.[2] The power from turbines increases as the cube of the fluid speed, (if the speed doubles, times as much power comes out). The law of energy conservation shows that the increased speed comes while decreasing the pressure.[3]

These Venturi effect devices, like the one shown in Figure 2, can be placed in relatively shallow water to take advantage of tidal power that otherwise wouldn't be available. Shallow ocean water often moves as a result of tides. The symmetry of the Venturi tube allows energy to be harnessed as the tide comes in or out.
For Further Reading
- Tidal power
- Tidal barrage
- Tidal stream generator
- Wind power
- Bernoulli's equation
- Betz limit
- Or explore a random page
References
- ↑ Wikimedia Commons [Online], Available: https://upload.wikimedia.org/wikipedia/commons/5/54/Venturifixed2.PNG
- ↑ 2.0 2.1 Neil and Hashemi, Fundamentals of Ocean Renewable Energy : Generating Electricity from the Sea pg 71m Elsevier, 2018
- ↑ It's a neat relationship: , read more at Bernoulli's equation.
- ↑ Picture also available online http://www.aquaret.com/indexa15e.html?option accessed May 27th, 2021.

