Entropy
Entropy is a measure of the number of ways a thermodynamic system can be arranged, commonly described as the "disorder" of a system. This concept is fundamental to physics and chemistry, and is used in the Second law of thermodynamics, which states that the entropy of a closed system (meaning it doesn't exchange matter or energy with its surroundings) may never decrease. This means that the "multiplicity", or number of ways a system can be arranged will never decrease, and that the system will naturally tend to higher disorder. The maximum disorder of a system occurs when it is at thermal equilibrium, therefore, this is what all isolated systems will tend to over time.[2]
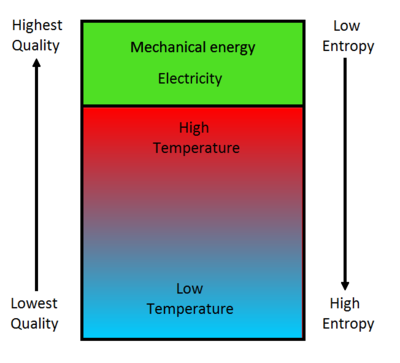
Entropy can also be described as a system's thermal energy per unit temperature that is unavailable for doing useful work.[3] Therefore entropy can be regarded as a measure of the effectiveness of a specific amount of energy. Shown in Figure 1, this is represented as the "energy quality", which decreases as the entropy of a system increases.[1] It can be seen that heat has a lower energy quality than mechanical energy or electricity, so this can be used to understand why an amount of heat cannot be converted completely into the same amount of these higher quality forms of energy.
In a reversible thermodynamic process, such as a Carnot engine, the change in entropy over a full cycle must be equal to zero. This can be explored in more detail on the Hyperphysics website.
Order out of Chaos

There are many examples of complexity in our world around us. Things such as
- Plants growing from tiny seeds,
- Single-celled fertilized eggs growing into complex life,
- Complex molecules and formations, and
- Vast increases of knowledge and information
are extremely complex systems which appear to violate the Entropy Statement of the Second law of thermodynamics.
Since entropy is increasing, and the Second law entails that out of this increase comes disorder, randomness and simplicity, how is it that there is so much order and complexity around us?
This is a major confusion in understanding entropy, and it is important to distinguish between an isolated (closed) and non-isolated (open) system. Open systems are free to interact with their environment, and therefore energy can be added to or removed from them. Systems that become more ordered as time passes are called self-organizing systems.[5] In order for this decrease in entropy to be possible, they must take in energy from an outside source. However, because the open system's entropy is decreasing, there must be an increase of entropy outside of the system.
For example, this is why water can freeze into complex structures. The water forms a highly organized crystal, and the entropy of the water decreases as it forms this structure. This happens because heat energy is transferred from the water to the surrounding air, therefore increasing the entropy of the air. This increase in the air must be more than the decrease in the water, because the whole system's entropy must increase. This is analogous to refrigeration, as work must be input to the refrigerator in order to cool it down, therefore decreasing its entropy.[5]
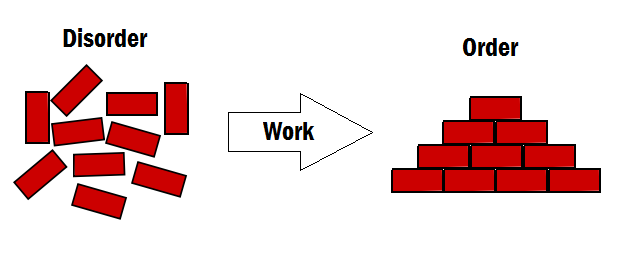
This concept of decreasing a non-isolated system's entropy can be visualized in Figure 3 below. (The arrangement of the bricks is not a literal representation of the brick's entropy, rather it is just to demonstrate the idea of "multiplicity". The actual entropy of the bricks has to do with their internal temperature.[6])
Entropy as the arrow of time
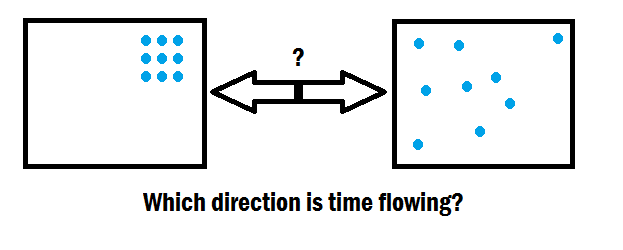
Since the entropy of a system tends to more disorder over time, and never in reverse, it is said to give us "time's arrow". If snapshots of a system at two different times shows one state which is more disordered, then it could be implied that this state came later in time.[7]
For Further Reading
- Thermodynamics
- First law of thermodynamics
- Second law of thermodynamics
- Thermal equilibrium
- Thermodynamics
- Or explore a random page
References
- ↑ 1.0 1.1 R. Wolfson, "Entropy, Heat Engines, and the Second Law of Thermodynamics" in Energy, Environment, and Climate, 2nd ed., New York, NY: W.W. Norton & Company, 2012, ch. 4, sec. 7, pp. 81-84
- ↑ Hyperphysics, A More General View of Temperature [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/temper2.html
- ↑ Encyclopaedia Britannica, Entropy [Online], Available: http://www.britannica.com/EBchecked/topic/189035/entropy
- ↑ Wikipedia Commons [Online], Available: http://upload.wikimedia.org/wikipedia/commons/b/ba/Flower_jtca001.jpg
- ↑ 5.0 5.1 R. D. Knight, "Order Out of Chaos" in Physics for Scientists and Engineers: A Strategic Approach, 3nd ed. San Francisco, U.S.A.: Pearson Addison-Wesley, 2008, ch.18, pp. 557
- ↑ Hyperphysics, Entropy as Time's Arrow [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/therm/entrop.html#e2
- ↑ Hyperphysics, Second Law: Entropy [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/seclaw.html#c4
- ↑ Adapted from Hyperphysics, Entropy as Time's Arrow [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/therm/entrop.html#e2