Carnot efficiency

Figure 1: A hot source provides the energy needed to produce work in a thermodynamic process. The Carnot efficiency depends only on the temperature of the hot source and the cold sink.

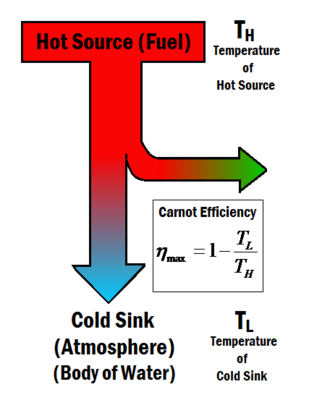
Carnot efficiency describes the maximum thermal efficiency that a heat engine can achieve as permitted by the Second Law of Thermodynamics. The law was derived by Sadi Carnot in 1824. Carnot pondered the idea of maximum efficiency in a heat engine questioning whether or not the efficiency of a heat engine can approach 100%, or is there an upper limit that cannot be exceeded? The answer turned out to be that there is a maximum value, and Carnot developed an ideal engine that would theoretically give this efficiency, known as the Carnot engine. The maximum efficiency, known as the Carnot efficiency [math]\eta_{max}[/math], is dependent only on the temperatures of the hot source and the cold sink [math]T_H[/math] and [math]T_L[/math], as shown in Figure 1, and is given by the equation below

(1)

[math]\eta_{max}=1-\frac{T_L}{T_H}[/math]

The Second Law requires that waste heat be produced in a thermodynamic process where work is done by a heat source. Such a process is given by the equation

(2)

[math]Q_H=Q_L+W[/math]

With a thermal efficiency of

(3)

[math]\eta=\frac{W}{Q_H}[/math]

Where:

• [math]Q_H[/math] is the heat supplied to the system from a fuel
• [math]Q_L[/math] is the heat given off by the system to the cold sink known as waste heat
• [math]W[/math] is the useful work achieved by the system

Therefore the Carnot efficiency gives a maximum attainable amount of work from any heat engine. It can be seen from Equation 1 that by either raising [math]T_H[/math] or lowering [math]T_L[/math] the efficiency can be increased. Ideally one would therefore want to make the cold sink temperature equal to absolute zero, but this is known to be impossible. In reality, the cold sink is the Earth's environment. This means that the cold sink is at a temperature of around 280-300 Kelvin, and the hot sources are from burning fuels burn at a temperature of approximately 1100 Kelvin (although research always tries to drive that temperature higher). These temperatures give a Carnot efficiency value of [math]\eta_{max} \approx 70\%[/math] or so.

Carnot Engine

A Carnot engine is an idealized engine, using processes that have reversible mechanical and thermal interactions. This means that the engine can go through its motions and return to its initial state without an increase in entropy (without energy loss). For the engine to be able to return to its initial state without increasing the entropy, the engine must be in thermal equilibrium throughout its cycle. The conditions for such an engine to exist are:

• Mechanical interactions: no energy is lost in the form of friction, therefore there is no heat transfer during these mechanical processes ([math]Q=0[/math]), known as an adiabatic process.

• Thermal interactions: the heat transfer is infinitely slow (known as a quasi-static). This means that the temperature difference between the system and the input/output heat is very nearly the same, causing the heat transfer to take place over an infinite amount of time. These exchanges must be done by keeping the internal temperature of the system constant, known as an isothermal process.

An engine that only possesses these properties is known as a Carnot engine, which is a "perfectly reversible engine", and exhibits the maximum thermal efficiency ([math]\eta_{max}[/math]) and, if operated as a refrigerator, coefficient of performance ([math]K_{max}[/math]). Although such an engine would maximize efficiency, in terms of effectiveness it is terribly impractical since its idealized processes take so much time to output a significant amount of work. As Schroeder puts it, "don’t bother installing a Carnot engine in your car; while it would increase your gas mileage, you’d be passed by pedestrians".

To learn more about the Carnot engine, visit NASA or hyperphysics.