Thermal efficiency
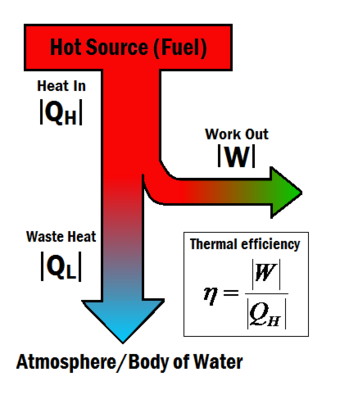
Heat engines turn heat into work. The thermal efficiency expresses the fraction of heat that becomes useful work. The thermal efficiency is represented by the symbol , and can be calculated using the equation:
Where:
is the useful work and
is the total heat energy input from the hot source.[2]
Heat engines often operate at around 30% to 50% efficiency, due to practical limitations. It is impossible for heat engines to achieve 100% thermal efficiency () according to the Second law of thermodynamics. This is impossible because some waste heat is always produced produced in a heat engine, shown in Figure 1 by the term. Although complete efficiency in a heat engine is impossible, there are many ways to increase a system's overall efficiency.
An Example
If 200 joules of thermal energy as heat is input (), and the engine does 80 J of work (), then the efficiency is 80J/200J, which is 40% efficient.
This same result can be gained by measuring the waste heat of the engine. For example, if 200 J is put into the engine, and observe 120 J of waste heat, then 80 J of work must have been done, giving 40% efficiency.
Carnot Efficiency
There is a maximum attainable efficiency of a heat engine which was derived by physicist Sadi Carnot. Following laws of thermodynamics the equation for this turns out to be
Where
is the temperature of the cold 'sink' and
is the temperature of the heat reservoir.
This describes the efficiency of an idealized engine, which in reality is impossible to achieve.[3] From this equation, the lower the sink temperature or the higher the source temperature , the more work is available from the heat engine. The energy for work comes from a decrease in the total energy of the fluid used in the system. Therefore the greater the temperature change, the greater this decrease in the fluid and thus the greater energy available to do work is.[4]
For Further Reading
For further information please see the related pages below:
- Heat engine
- Hydrocarbon combustion is often the source of heat for these engines.
- Solar thermal power plant
- Nuclear power plant
- For thermal efficiency of car engines, click here
- Or explore a random page!
References
- ↑ This picture was made by the Energy Education team.
- ↑ TPUB Engine Mechanics. (April 4, 2015). Thermal Efficiency [Online]. Available: http://enginemechanics.tpub.com/14075/css/14075_141.htm
- ↑ Hyperphysics, Carnot Cycle [Online], Available: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/carnot.html
- ↑ R. A. Hinrichs and M. Kleinbach, "Heat and Work," in Energy: Its Use and the Environment, 4th ed. Toronto, Ont. Canada: Thomson Brooks/Cole, 2006, ch.4, sec.E, pp.115

